Schaltnetzteile
Lösungen zu den Aufgaben




  1. Aufgabe: Gleichrichter

    2. a) Mit C = i · Δt / ΔU   folgt   C115/50 = 4µF/W
    Der Strom verdoppelt sich und ΔU muß halbiert werden)
    b) C115/60 = 3.33µF/W

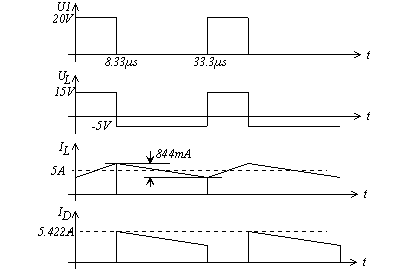
  2. Aufgabe: Abwärtswandler

    1. t1/T = 0.5 ... 0.125
    2. IDrain_max = 5.5A
    3. IDiode_max = 5.5A
    4. L = 145.8 µH

    5. 010419i


  3. Aufgabe: Abwärtswandler

    4. a) f = 250kHz; b) Ua=5V; c) Ue=10V; d) L=2uH, e) Ia=12.5A; f) Ie=6.25A; g) und h) Pa=Pe=62.5W

  4. Aufgabe: Abwärtswandler

    1. t1/T = 0.5 ... 0.25
    2. Für Ue = 20 V entsteht die größte Stromwelligkeit in der Drossel: L = 187,5μH

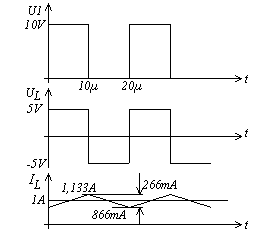
    3. 010420a
    4. Der ungünstigste Fall tritt ein bei Ue =20V. Mit ΔIL = 0,4A folgt Iamin = 0,2A


  5. Aufgabe: Abwärtswandler

    1. Ue = 40V, Ua = 20V
    2. f = 83,3 kHz
    3. L = 20μH
    4. Ie = 0,66A, Ia = 1,33A


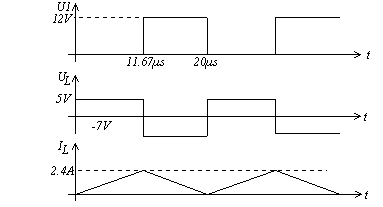
  6. Aufgabe: Aufwärtswandler

    1. t1/T = 0.5883;
    2. IC_max = 2.4A
    3. IDiode_max = 2.4A
    4. L = 24.3µH

    5. 010419j


  7. Aufgabe: Aufwärtswandler

    8. a) f=50kHz; b) Ua=600V; c) Ue=300V; d) L=3mH; e) Ia=1.25A; f) Ie=2.5A; g,h) Pa=Pe=750W

  8. Aufgabe: Aufwärtswandler

    1. Ue = 30V, Ua = 40V
    2. f = 83,33kHz
    3. L = 30μH
    4. Ie = 0,66A, Ia = 0,5A


  9. Aufgabe: Sperrwandler

    1. Î1 = 4·Pa / Ue_min = 0,3A
      UDS = Ue + Ua· N1 / N2

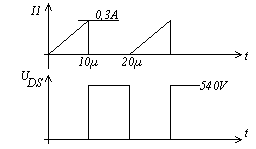
      010420b
    2. L1 = Ue2 / (8 Pa·f)   mit Ue = Ue_min    folgt   L1 = 9,11mH
      N1 / N2 = Ue_min / Ua = 1,35
    3. Bei Ue_max, dann wird UDS = Ue_max + Ua· N1 / N2 = 360V + 270V = 630V
    4. Der Wandler arbeitet immer im lückenden Betrieb, also auch bei Ue = 360V, weil er bereits bei minimaler Eingangsspannung an der Grenze zum lückenden Betrieb ist.


  10. Aufgabe: Sperrwandler

    1. Mit C' = 1μF/W   wird C = C'·140W = 140μF,   gewählt: 150μF
    2. Annahme: Ue_min = ca. 260V, Î1 = 2,87A, L1 = 0,9mH
    3. ETD 44 mit g = 1,5mm: N1 = SQRT (L1 / AL) = SQRT (0,9mH / 194nH) = 68, Kontrolle Bmax = (AL·N1·Î1) / Amin = 222mT
      Übrigens: Der Kern ETD39 mit 1mm Luftspalt hätte fast auch gereicht: Bmax = 306mT
      N2 = N1·Ua + 0,7V / Ue_min = 68·5,7V/260V = 1,5 (gewählt 2), N3 = N2·15,7V / 5,7V = 5,5 (gewählt 6) und N4 = N2·300V / 5,7V = 210
    4. Bei maximaler Eingangsspannung wird der Transistor am höchsten belastet: UDS_max = Ue_max + Ua· N1 / N2 = 360V + 260V = 620V


  11. Aufgabe: Sperrwandler

    1. L1 = Ue·Δt/ΔIL = 300V·10μs/0,5A = 6mH
    2. Das Tastverhältnis ist 0,5, damit ist N1 / N2 = Ue / (Ua + 0,7V = 19
    3. Leistungsbilanz: Ia = avg(Ie)·300V/15V = 372mA·300V/15V = 7,5A
      (Es sei hier vermerkt, daß der Wirkungsgrad von η=1 bei diesem Windungszahlenverhältnis in der Praxis bei weitem nicht erreicht werden kann, wegen der schlechten Kopplung der Wicklungen. Ein Wirkungsgrad von 70% wäre realistisch.)


  12. Aufgabe: Sperrwandler

    1. Ue = 300V
    2. L1 = Ue·Δt / ΔI = 750μH
    3. UDS = Ue + Ua· N1 / N2. Mit Ue = 300V wird Ua· N1 / N2 = UDS - Ue = 500V - 300V = 200V. Daraus folgt: N1 / N2 = 200 / 300 = 0,666
    4. η = Pa / Pe = 300V·150mA / (300V·200mA) = 0,75, wobei der Mittelwert des Eingangsstromes 200mA beträgt.


  13. Aufgabe: Speicherdrossel

    14. Berechnungsweg: Man wählt nach gutdünken einen Kern aus, berechnet die notwendige Windungszahl und kontrolliert danach, ob der Kern bei dem maximalen Strom unter Bmax = 0,3T bleibt. Falls Bmax größer als 0,3T wird, muß ein größerer Kern gewählt werden. Falls Bmax deutlich unter 0,3T bleibt, sollte nach einem kleineren, preisgünstigeren Kern gesucht werden.

    Lösung: ETD54, g = 2mm: N1 = SQRT (L1 / AL) = SQRT (1mH / 229nH) = 66, Kontrolle: Bmax = (AL·N1·Î1) / Amin = 270mT


  14. Aufgabe: Speicherdrossel

    15. Nmax = Bmax·Amin / (AL·Imax) = 88;   →  L = 1,5mH

  15. Aufgabe: Speicherdrossel

    1. L = 419,2μH
    2. Imax = 4,9A
    3. N = 32


  16. Aufgabe: Speicherdrossel

    1. ETD 44, g = 1,5mm: N = 71,   Bmax = 240mT    oder
      ETD 44, g = 1,0mm: N = 62,   Bmax = 281mT
    2. mit ETD 44, g = 1,5mm: Lmax = 1,5mH
      mit ETD 44, g = 1,0mm: Lmax = 1,1mH