| Hauptseite | | weiterführende Literatur | | Verwendung | | Tips | |
| Seitenanfang | | Benutzung d. Programms | | mathematische Grundlagen | | Funtionsprinzip | | Hilfe zu Spulendaten |
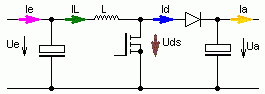
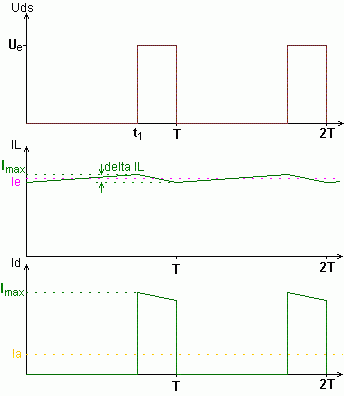 kontinuierlicher Betrieb |
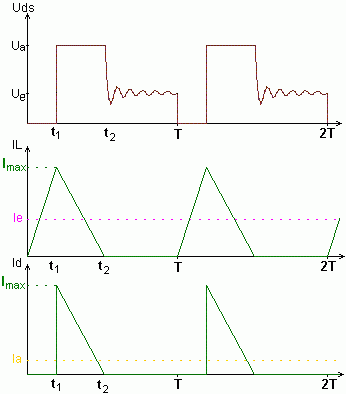 diskontinuierlicher Betrieb |
| Hauptseite | | weiterführende Literatur | | Verwendung | | Tips | |
| Seitenanfang | | Benutzung d. Programms | | mathematische Grundlagen | | Funtionsprinzip | | Hilfe zu Spulendaten |