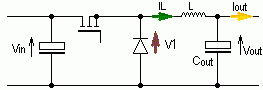
Buck Converter

How to use the program

Reference: The shapes of current and voltage curves are calculated using Faraday's Law. They do not represent an incremental simulation like it is done normally by programs like P-Spice. In the calculations the forward voltages of the diodes are considered with V_F = 0.7V, and the transistors are interpreted as ideal switches.

The values of all input fields can be changed.
If an input field is left empty, a default value is chosen. This value is displayed after leaving the input field in question.
The switch mode power supply operates within a certain input range i.e. between V_{in_min} and V_{in_max}.
The program needs the output values V_out and I_out.
The switching frequency f is the operating frequency of the transistor.
If the field "proposal" is activated, the proposed choking coil L and the current ripple ΔI_L are chosen such that ΔI_L = 0.4I_out, for V_{in_max} as the input voltage.
If you should not be content with the proposed values, you can change L or ΔI_L. If this is the case, the field "proposal" is deactivated automatically.
The value V_in is the value for the calculation of the current and voltage diagrams on the right side of the display. V_in must lie between V_{in_min} and V_{in_max}.

Top of page

Application:

The Buck Converter converts an input voltage to a lower output voltage. The buck converter often replaces the traditional analogue voltage regulator.

Top of page

Function principals

Illustration 1: Buck Converter

The transistor works as a switch which is driven by a high frequency pulse-width-modulated control voltage. The switch is turned on and off by the pulse-width-modulated control voltage. The ratio between on-time and the period t₁/T is called the Duty Cycle.

For the following analysis it will be assumed that the transistor is simplified as an ideal switch and the diode has no forward voltage drop. In the program itself, the diode will take into account a forward voltage drop V_F = 0.7V.

During the on-time of the transistor, the voltage V₁ is equal to V_in. Since V_in is higher than V_out the current through the diode increases linearly in correspondence to Faraday's Law.
When the transistor is turned off (blocking phase) the diode takes the inductor current. At this time the voltage across the inductor inverts. The voltage V₁ becomes zero (exact: -0.7V) and the voltage across the inductor is now -V_out. The inductor current I_L decreases linearly. If the current I_L does not decrease to zero during the blocking phase, this is called continuous mode (see illustration 2).

In this mode V₁ is a voltage which changes between V_in and zero, corresponding to the duty cycle t₁/T. The Low Pass Filter, formed by L and C_out, produces an output voltage equivalent to the average value of V₁, i.e. V_out = V₁.

For the continuous mode the output voltage is a function of the duty cycle and input voltage, it is independent of the load.

The inductor current I_L has a triangular shape, its average value is determined by the load. The peak to peak current ripple ΔI_L is dependent on L and can be calculated with the help of Faraday's Law. For V_out = (t₁/T) · V_in and a switching frequency f it follows that for continuous mode:

Eqn 2

The current ripple ΔI_L is independent of the load. The output current I_out is equal to the average value of the inductor current I_L.

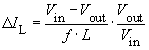
At low load current, namely if I_out < ΔI_L/2, the inductor current I_L falls to zero during every switching cycle. This mode is called discontinuous mode (see illustration 2). For this mode the calculations above are not valid.

At the moment when the inductor current becomes zero, i.e. t₂, the voltage V₁ jumps to the value of V_out because in this case V_L = 0. The drain-source capacitance in parallel with the diode-junction capacitance forms a resonant circuit with the inductance L. This is stimulated by the voltage jump across the diode. The voltage V₁ then oscillates and fades away.

Continuous Mode

Discontinuous Mode

Illustration 2: Operating modes of the Buck Converter

Top of page

Tips

The larger the chosen value of the inductor L, the smaller the current ripple ΔI_L. However this results in a physically larger and heavier inductor.
Choose ΔI_L so that it is not too big. The suggestions proposed by us have adequately small current ripple along with physically small inductor size. With a larger current ripple, the voltage ripple of the output voltage V_out becomes clearly bigger while the physical size of the inductor decreases marginally.
The higher the chosen value of the switching frequency f , the smaller the size of the inductor. However the switching losses of the transistor also become larger as f increases.
The smallest possible physical size for the inductor is achieved when ΔI_L = 2I_out at V_{in_max}. However, the switching losses at the transistors are at their highest in this state.

Top of page

Mathematics used in the program

The following parameters must be entered into the input fields:

V_{in_min}, V_{in_max}, V_out, I_out and f

Using these parameters, the program produces a proposal for L:

_out

For the calculation of the curve-shapes, and also for the calculation of "ΔI_L for V_{in_max}", two cases have to be distinguished, i.e. continuous mode and discontinuous mode:

From this it follows that:

For ΔI_L< 2I_out the converter is in continuous mode and it follows that:
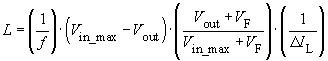
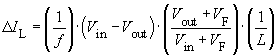
For ΔI_L> 2I_out the converter is in discontinuous mode and it follows that:

,

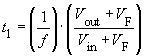
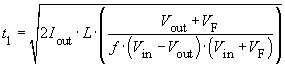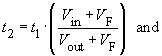
Main page \|	How to use the program \|	Function principals \|	Mathematics used in the program \|
Top of page \|	Application \|	Tips \|	Literature Notes \|	Help for choking coils