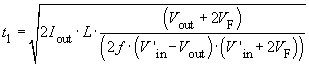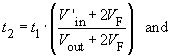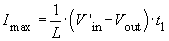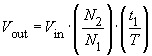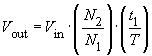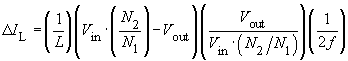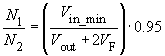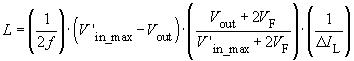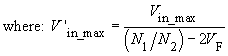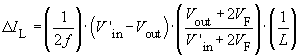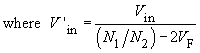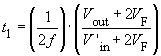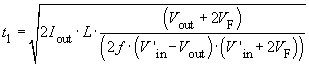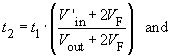Full-Bridge Push-Pull Converter
How to use the program
Reference: The shapes of current and voltage curves are calculated using Faraday's Law. They do not represent an incremental simulation like it is done normally by programs like P-Spice. In the calculations the forward voltages of the diodes are considered with VF = 0.7V, and the transistors are interpreted as ideal switches.
- The values of all input fields can be changed.
- If an input field is left empty, a default value is chosen. This value is displayed after leaving the input field in question.
- The switch mode power supply operates within a certain input range i.e. between Vin_min and Vin_max.
Note:
- For the european mains of 230V +/-10% and behind the rectifier and the smoothing (with a voltage ripple of 10%) the input voltage range is between Vin_min = 250V and Vin_max = 360V.
- For wide range Switch Mode Power Supplies the input voltage range of the mains is from 100Vac -10% (Japan) to 240Vac +6% (Great Britain). In this case, the DC input range of the power supply is from Vin_min = 110V to Vin_max = 360V.
- For use of a power factor pre-regulator the input voltage range is normally from Vin_min = 360V to Vin_max = 400V.
- The program needs the output values Vout and Iout.
- The switching frequency f is the operating frequency of the transistor.
- If the field "proposal" is activated for the inductor L, a value for L and the corresponding current ripple ΔIL is proposed. These values are laid out such that ΔIL = 0.4Iout with Vin_max as the input voltage.
- If the field "proposal" for the input field "N1/N2" is activated, the turns ratio N1/N2 is proposed. This suggestion is chosen such that the required output voltage can be achieved using Vin_min as an input voltage.
- If you do not agree with our proposals, you can change N1/N2 or L as well as ΔIL. The field "proposal" is then deactivated automatically.
- The value Vin is the value for the calculation of the current and voltage diagrams on the right side of the display. Vin must lie between Vin_min and Vin_max.
Top of page
Application
The Full-Bridge Push-Pull Converter belongs to the primary switched converter family since there is isolation between input and output. It is suitable for very high output powers.
Top of page
Function principals
|
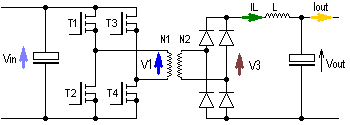
Illustration 1: Full-Bridge Push-Pull Converter
|
For the following analysis it will be assumed that the transistor is simplified as an ideal switch and the diode has no forward voltage drop. In the program itself, the diode will take into account a forward voltage drop VF = 0.7V.
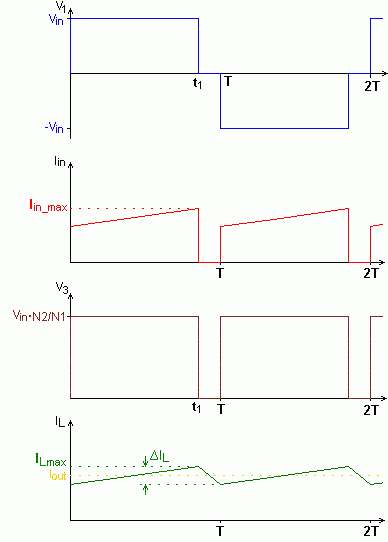
The Push-Pull converter drives the high-frequency transformer with an AC voltage, where the negative as well as the positive half swing transfers energy.
The primary transformer voltage V1 can be +Vin, -Vin or zero depending on which pair of transistors (T1,T4 or T2,T3) are turned on or off.
On the secondary side, the AC voltage is rectified, so that V3 is a pulse-width-modulated control voltage which switches between Vin.(N2/N1) and zero. Due to the rectification, the pulse-frequency of V3 is equal to 2· f .
The Low-Pass filter, formed by the inductor L and the output capacitor Cout, produces the average value of V3. For continuous mode (IL never becomes zero) this leads to:
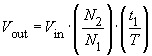
The Duty cycle of this converter may theoretically increase to 100%. In practice this is not possible because the serial connected transistors T1 and T2, have to be switched with a time difference to avoid a short circuit of the input supply.
Due to the fact that the duty cycle t1/T can theoretically increase to 100%, a condition for the turns ratio emerges:

In the program, this value is multiplied by a factor of 0.95, so that the proposed value for N1/N2 includes a small margin which guarantees the demagnetisation of the core, when the input voltage is minimal, (remember: at minimum input voltage the duty cycle reaches its maximum).
For the allocation of the inductor L, the same rules as for the
Buck Converter can be used. One also distinguishes between discontinuous and continuous mode, depending on whether or not the inductor current falls to zero during the on-time of the transistor.
During continuous operation:
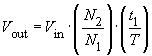
- In continuous mode the output voltage depends only on the duty cycle and the input voltage, it is load independent.
The inductor current IL has a triangular shape and its average value is determined by the load. The change in inductor current ΔIL is dependent on L and can be calculated with the help of Faraday's Law.
During continuous mode, with Vout = Vin · (N2/N1) · t1/T and a chosen switching frequency f it can be shown that:
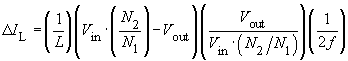
- The change in inductor current is load independent. The output current Iout is taken to be the average value of the inductor current IL.
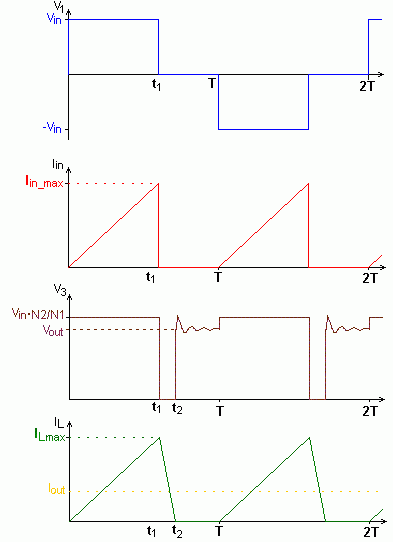
For a small load current, namely if Iout < ΔIL/2, the current will fall to zero during every period. This is what is known as discontinuous mode. In this case the calculations stated above are no longer valid.
In that moment, when the inductor current becomes zero, the voltage V3 jumps to the value of Vout. The diode junction capacitance of the secondary rectifier forms a resonant circuit with the inductance, which is activated by the voltage jump at the rectifier. The voltage V3 then oscillates and fades away.
| 
|
Continuous Mode
| Discontinuous Mode
|
Illustration 2: Operating modes of the Full-Bridge Push-Pull Converter
Top of page
Tips
- The larger the chosen value of the inductor L, the smaller the current ripple ΔIL. However this results in a physically larger and heavier inductor.
- The higher the chosen value of the switching frequency f , the smaller the size of the inductor.
However the switching losses of the transistor also become larger as f increases.
- The smallest possible physical size for the inductor is achieved when ΔIL = 2Iout at Vin_max. However, the switching losses at the transistors are at their highest in this state.
- Choose ΔIL so that it is not too big. The suggestions proposed by us have adequately small current ripple along with physically small inductor size. With a larger current ripple, the voltage ripple of the output voltage Vout becomes clearly bigger while the physical size of the inductor decreases marginally.
- It is best not to alter the turns ratio N1/N2 proposed by us.
Top of page
Mathematics used in the program
The following parameters must be entered into the input fields:
Vin_min, Vin_max, Vout, Iout and f
Using these parameters, the program produces a proposal for N1/N2 and L:
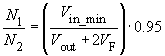
(the factor of 0.95 is taken into account to allow for the fact that the duty cycle t1/T = 1 cannot be completely reached).
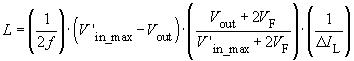
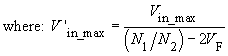
VF = 0.7 (Diode Forward-voltage)
ΔIL = 0.4Iout
For the calculation of the curve-shapes, and also for the calculation of "ΔIL for Vin_max", two cases have to be distinguished, i.e. continuous mode and discontinuous mode:
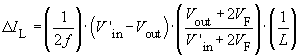
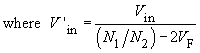
From this it follows that:
- For ΔIL< 2Iout the converter is in continuous mode and it follows that:
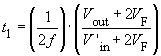
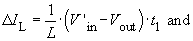
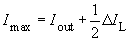
- For ΔIL> 2Iout the converter is in discontinuous mode and it follows that: